Algoritmos de busca sequencial e binaria

Busca Sequencia ou Linear

Quando itens de dados são armazenados em uma coleção, como uma lista, dizemos que eles têm uma relação linear ou sequencial. Cada item de dados é armazenado em uma posição relativa aos outros. Nas listas (vetores) JavaScript, essas posições relativas são os valores de índice dos itens individuais. Como esses valores de índice são ordenados, é possível para nós visitá-los em sequência. Este processo dá origem a nossa primeira técnica de busca, a busca sequencial.

A imagem abaixo mostra como essa pesquisa funciona. A partir do primeiro item da lista, simplesmente passamos de item para item, seguindo o pedido sequencial subjacente até encontrar o que estamos procurando ou ficar sem itens. Se ficarmos sem itens, descobrimos que o item que procuramos não estava presente.

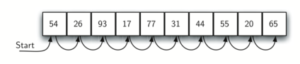
Para a implementação do código em JavaScript. A função precisa da lista e do item que procuramos e retorna um valor booleano para saber se ele está presente. A variável booleana encontrada é inicializada para falso (false) e é atribuído o valor verdadeiro (true) se descobrimos o item na lista.

function buscaSequencial(umVetor, item){
    let pos = 0;
    let achou = false;

    while(pos < umVetor.length && !achou){
        if (umVetor[pos] === item){
            achou = true;
        }
        else{
            pos = pos+1;
        }
    }

    return achou;
}

Análise de Complexidade

No melhor caso, o elemento a ser buscado é encontrado logo na primeira tentativa da busca. No pior caso, o elemento a ser buscado encontra-se na última posição e são feitas N comparações, sendo N o número total de elementos. No caso médio, o elemento é encontrado após (N+1)/2 comparações. O algoritmo de busca linear é um algoritmo O(n).

Busca binaria

Caso você possua uma lista com os valores ordenados de forma numérica ou alfabética, é possível fazer uma busca muito mais rápida. Ao invés de pesquisar a lista em sequência, uma busca binária começará examinando o item do meio. Se esse item for aquele que estamos procurando, a busca termina. Se não for o item correto, podemos usar a natureza ordenada da lista para eliminar a metade dos itens restantes. Se o item que procuramos for maior do que o item do meio, sabemos que toda a metade inferior da lista, bem como o item do meio, podem ser eliminados de uma consideração mais aprofundada. O item, se estiver na lista, deve estar na metade superior.

Podemos então repetir o processo com a metade superior. Comece no item do meio e compare-o contra o que estamos procurando. Novamente, encontramos ou dividimos a lista pela metade, eliminando assim uma grande parte do nosso possível espaço de busca. A Figura abaixo mostra como esse algoritmo pode encontrar rapidamente o valor 54.

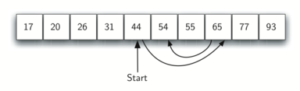
function buscaBinaria(umVetor, item) {
    let prim = 0;
    let ult = umVetor.length - 1;
    let achou = false;

    while (prim <= ult && !achou) {
        meioLista = Math.ceil((prim + ult) / 2);
        if (umVetor[meioLista] == item) {
            achou = true;
        }
        else {
            if (item < umVetor[meioLista]) {
                ult = meioLista - 1;
            }
            else {
                prim = meioLista + 1;
            }
        }
    }
    return achou;
}

Análise de Complexidade

A complexidade desse algoritmo é da ordem de Θ(log2 n), em que n é o tamanho do vetor de busca. Apresenta-se mais eficiente que a Busca linear cuja ordem é O(n).